最大堆、最小堆、堆排序、代码实现。
# Lecture06-Proiority Queues 优先级队列
# 概述
A priority queue is a collection of zero or more elements. Each element has a priority or value.
一个优先级队列是 0 个或者更多元素的集合。每一个元素都有一个优先级或者值
进入队列的时候有优先级,出队列优先出高优先级的.
# 如何确定优先级
以下我们确定元素的优先级是通过数字的大小来确定。
In a min priority queue the find operation finds the element with minimum priority, while the delete operation delete this element.
在最小优先级队列中,当需要删除一个元素的时候,我们找到优先级最小的元素来删除
In a max priority queue, the find operation finds the element with maximum priority, while the delete operation delete this element.
在最大优先级队列中,当需要删除一个元素的时候,我们找到优先级最大的元素来删除
# ADT (逻辑上最大优先级队列)

# Heap
A max heap (min Heap):(最大堆)
is A complete binary tree
最大堆是一个完全二叉树
The value in each node is greater(less) than or equal to those in its children(if any).
每一个节点上的值都大于 (小于) 或者等于他的子节点 (如果有的话)
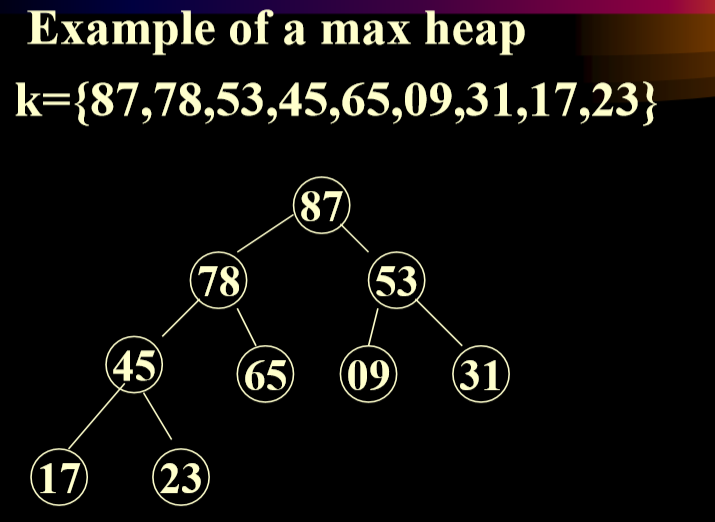
# 例子
最大堆:节点比自己的每个子节点都大
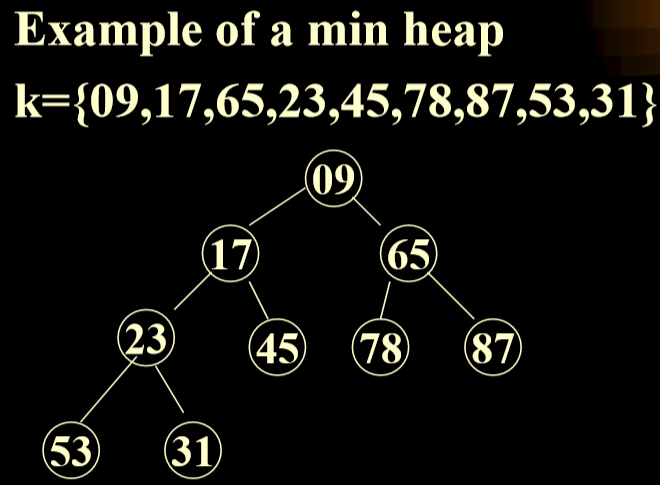
最小堆:节点比自己的每个子节点都笑
注意:完全二叉树可以用矩阵来进行存储。
- 从上向下一层一层进行记录。
# 最大优先级队列的代码实现

# 构造函数

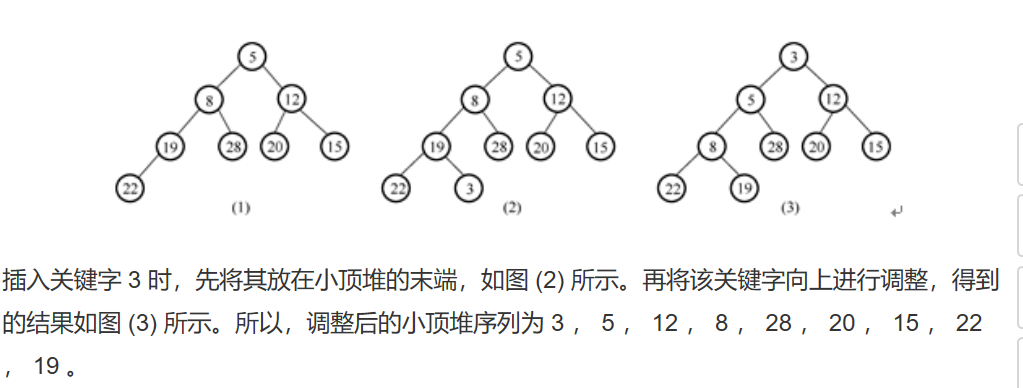
# 插入算法


首先,将插入元素插入到堆的最后;然后,经过反复操作【和父节点比优先级】,一直比较直到比父节点小为止。

用数组模拟完全二叉树,可以用常数时间复杂度求出它的父节点下标;
为什么堆排序中,i/2 是父节点?
直观感受:


推导:
利用等比数列求和
第 n 行的第 a 个元素在数组中下标为:2n + a - 1
第 n 行的第 2a - 1 和 2a 个元素在数组中的下标为:2n+1 + 2a 和 2n+1 + 2a - 1
# 删除算法

最大堆删除
树根删除,最后一个节点放到树根
下滤:左节点和右节点比较,较大的和父节点相比,如果父节点较大,循环结束,否则,换完继续和子节点比较。

ci < CurrentSize && heap[ci] < heap[ci + 1]
对比一下,左子节点和右子节点哪个更大。跟大的那个进行比较,不断进行下滤的操作。
# minHeap 的实现(cpp 代码实现)





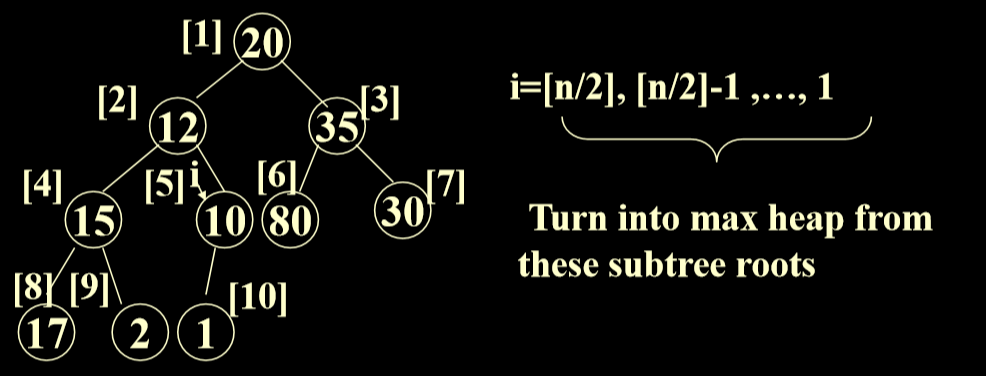
# 初始化一个非空的最大优先级数列(自底向上)
把初始指针指向最后一个节点的父结点 (N/2), 然后进行循环,然后每一个都换一遍就完成。
总体来讲是从最后一个节点的父结点开始,对所有的非叶节点进行下滤操作。


# 算法复杂度分析
对于不同层的节点,其下滤的计算量时不同的
如何从感觉上立即这个问题 —— 在数据的开始是不会到 lgn 的,而只有到后面的时候才能达到 lgn(lgn = log2n)
第 i 层需要交换 k-i 次,该层中有 2i 个结点
i 到 根的距离, j 到 叶的距离
O(n) 的算术复杂度
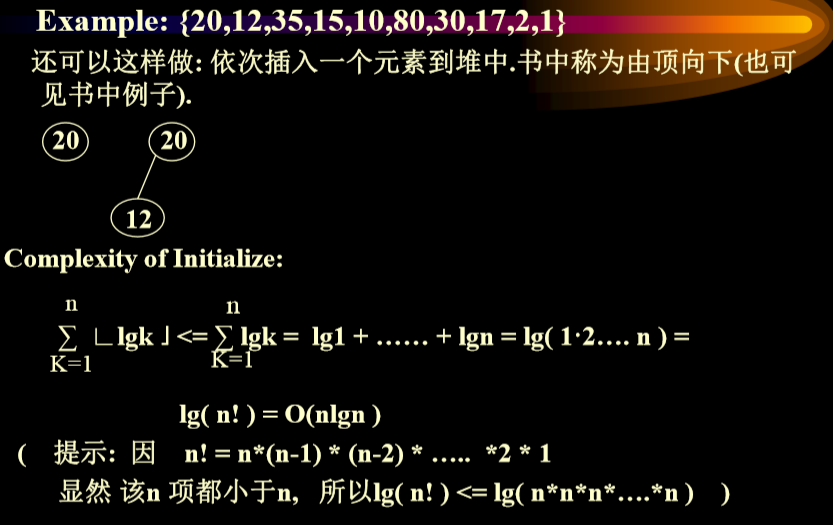
# 自上向下的初始化操作
最详细的最小堆构建、插入、删除的过程图解
# 优先级队列的应用
# 堆排序 (容易考)
# 复杂度分析
initialize a max heap with the n elements to be sorted O(n)
初始化一个 n 个元素的最大堆,O (n)
each time we delete one element, then adjust the heap O(log2n)
每次我们删除最大的元素,调整堆的时间复杂度为 O (log2n)
Time complexity is O(n)+O(nlog2n)= O(nlog2n)
对于所有情况,堆排序的复杂度都是
nlgn
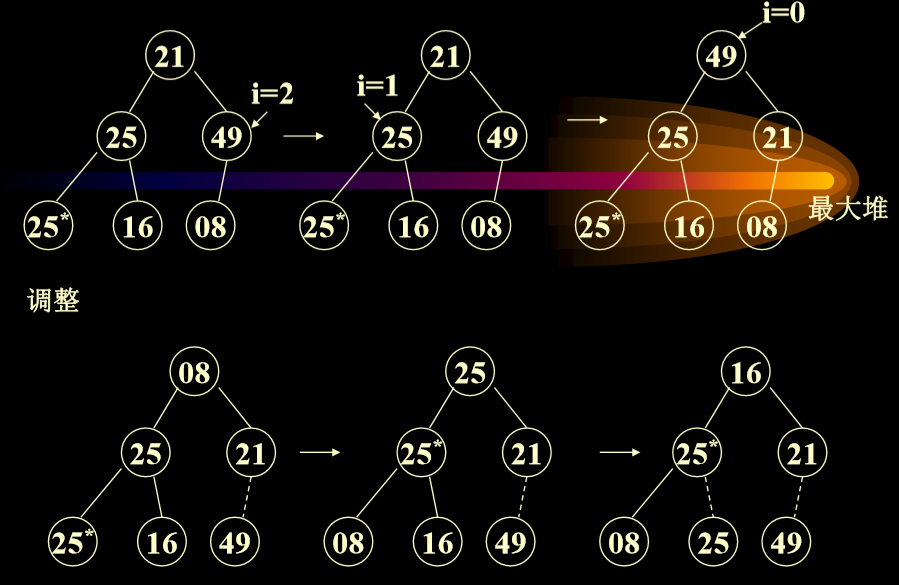
# 例子:
25 为什么有个星号?因为数组里面有两个 25
删除 49,8 放到根的位置,49 放到 8 的位置。
堆排序每次删除最大的,然后把最大的放到最下方节点,把节点交换到顶部后进行下滤算法。
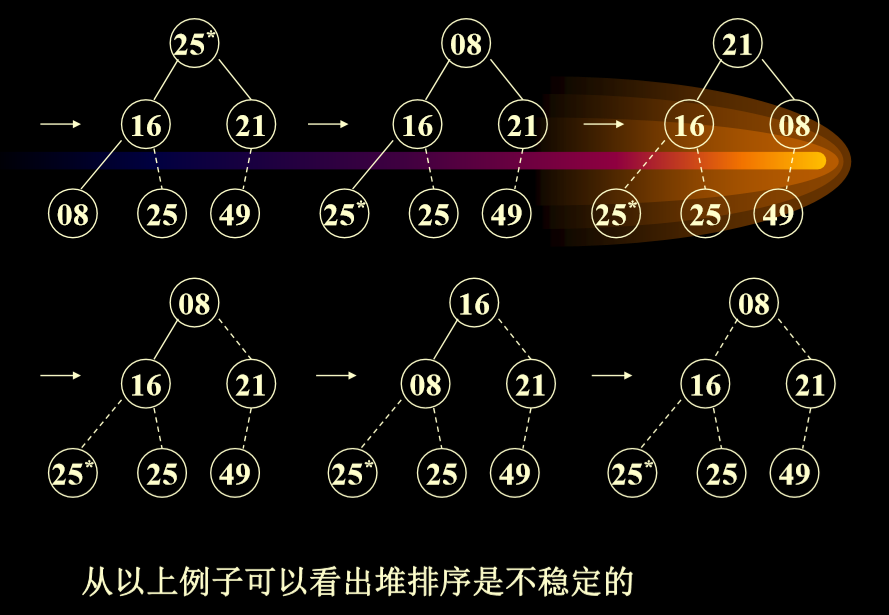
堆排序是不稳定的:因为相同数据的相对位置改变
稳定:25 25 的相对位置不变
不稳定:25 25 的相对位置改变
# 堆排序代码实现(?



堆排序可视化网站:
https://www.cs.usfca.edu/~galles/visualization/HeapSort.html
# The Selection Problem 查找问题
问题描述:在 N 个元素中找出第 K 个最大元素。
- 1A 算法:读入 N 个元素放入数组, 并将其选择排序,返回适当的元素。算法时间复杂度:O (N2)
- 1B 算法:
- 将 K 个元素读入数组,并对其排序 (按递减次序)。最小者在第 K 个位置上。
- 一个一个地处理其余元素:每读入一个元素与数组中第 K 个元素 (在 K 个元素中为最小) 比较,如果大于,则删除第 K 个元素,再将该元素放在合适的位置上 (调整过程)。如果小于,则舍弃。最后在数组 K 位置上的就是第 K 个最大元素。
- 运行时间 (1B 算法): O (K2 + (N - K)K ) = O( NK ) 当 K = N / 2 (向上取整), O ( N2)
- 例如:3, 5, 8, 9, 1, 10,找第 3 个最大元素。
# 4.2.1. 用堆来解决当前问题
- 6A 算法:假设求第 K 个最小元素
- 将 N 个元素建堆 (最小) O ( N )
- 执行 K 次 delete,O (K*logN) O ( N + K * log N )
- 如果 K = (N/2)(向上取整),O ( N * log N )
- 如果 K = N ,O (N * log N) 堆排序
- 如果是 N 取代最后一个是 nlgn,可以考虑使用不同的情况来确定建立最大堆还是最小堆。
- 6B 算法:假设求第 K 个最大元素
- 读入前 K 个元素, 建立最小堆 O (K)
- 其余元素一一读入:每读入一个元素与堆中第 K 个最大元素比 (实际上是堆中最小元素) O (1)
- 大于,则将小元素去掉 (堆顶),该元素进入,进行一次调整。O (log K )
- 小于,则舍弃。
- O( K + ( N-K) * log K ) = O( N*log K)
- 当 K = (N/2)(向上取整) , θ(N * log N )
- 对 6A, 6B, 用同样的数据进行测试, 只需几秒钟左右给出问题解。
# 例题:2009 统考题
- 答案:A
- 直接按照顺序一行一行生成。