不同的散列方式。
取余法、平方取中法、乘法杂凑法、线性探测法 linear probing、二次探测法 quadratic probing、双散列函数 double hashing、分离链接法 separate chainging。

# Lecture05 - 散列函数

# 简介

散列表 (Hash function/name-address function)

Address = hash (key)，将搜索的复杂度降到常数复杂度 O (C)

如何解决冲突？

α=n / b

n 是元素个数，b 是桶的数目

# 散列函数

# 取余法

大小通常取最大质数，避免造成散列中存在始终未用到的部分。

# 平方取中法

先进行原来的数据进行平方，然后取八进制，再选取中间的合适部分。

# 乘法杂凑函数

M 是表长？
用一个无理数乘 key 值然后丢掉整数得到小数部分。

# 针对字符串 - 1

to add up the ASCII (or Unicode) value of the characters in the string. 把字符串中的每一个字符的 ASCII 值或者 Unicode 值相加

	public static int hash( String Key, int tableSize ) {
	int hashVal = 0;
	for( int i = 0; i < Key.length( ); i++ )
	hashVal += Key.charAt( i );
	return hashVal % tableSize;
	}

如果字符串长度很短，那么会集中在前面的散列表

# 针对字符串 - 2

前面乘一个乘数，把数据打散

# 如何解决散列表冲突问题

碰撞的两个 (或多个) 关键码称为同义词，即 H (k1)=H (k2),k1 不等于 k2

# linear Probing (线性探测法)

If hash(key)= d and the bucket is already occupied then we will examine successive buckets d+1, d+2,……m-1, 0, 1, 2, ……d-1, in the array

如果 key 的哈希值是 d，并且 d 对应的位置已经被占据，然后我们会按照线性顺序向后成环形查找

散列表已经满了之后，算法复杂度比较高，需要遍历整个散列表

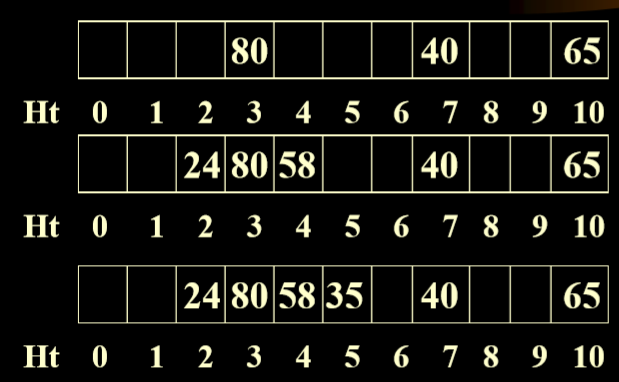
# 例一

放入 58 的时候和 80 冲突，因此放到下一个 4

同理，放入 35 的时候冲突

计算例一中的平均成功访问次数

58 查 2 次，35 查 4 次

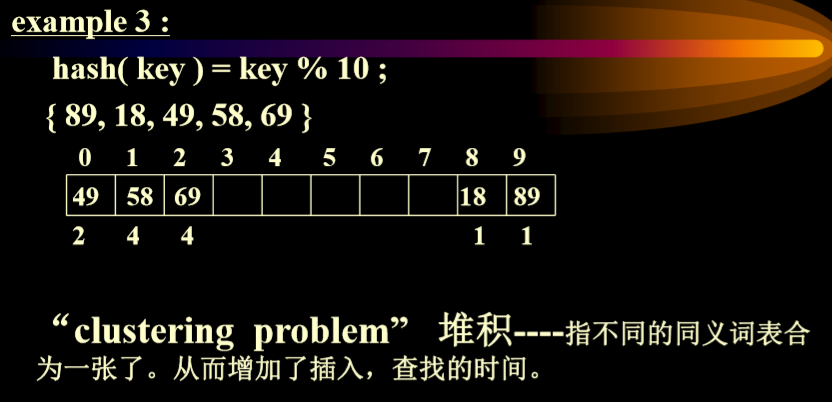
# 例二

线性表示法的弊端 —— 堆积问题

如果一个地方发生了冲突，那么周围的复杂度会迅速升高

查询 35 从位置 2 开始查询，不是的话查询下一个。如果 58 被删除，35 在寻访位置 4 的时候是空的，停止查询。

不能直接删除线性表中的数据，应该是进行标记，标志该元素已经删除。

# 线性探测法的 c++ 实现

	//hashtable 的构造方法
	template<class E,class K>//E 和 K 需要被实例化后，这个类才能被调用。
	HashTable<E,K>::HashTable(int divisor){
	D = divisor;
	ht = new E[D];
	empty= new bool[D];
	for(int i=0;i<D;i++)
	empty[i] = true;
	}

	template<class E,class K>
	int HashTable<E,K>::hSearch(const K&k)const {
	int i= % D;//home bucket
	int j= i ; //start at home bucket
	do {
	if(empty[j] \|\| ht[j]==k) return j;//fit
	j= (j+1) % D; //next bucket
	} while(j != i); //returned to home? 是否循环完成一遍
	return j; //table full;
	}

	// 参数进行引用 K&k
	template<class E,class K>
	bool HashTable<E,K>::Search(const K&k,E&e)const{
	//put element that matches k in e.
	//return false if no match.
	int b= hSearch(k);
	if(empty[b]\|\|Hash(ht[b])!=k)return false;
	e=ht[b];
	return true;
	}

	template<class E,class K>
	HashTable<E,K>& HashTable<E,K>::Insert(const E& e) {
	K k=Hash(e);//extract key
	int b=hSearch(k);
	if(empty[b]){
	empty[b]=false;
	ht[b]=e;
	return *this;
	}
	throw NoMem(); //table full
	}

# 二次探测法 (Quadratic probing)

quadratic 平方

注意，平方如果冲突之后，是在原来的位置 - 1， -4， -9 进行循环的

# 实现方法

	public interface Hashable {
	int hash(int tableSize);
	}
	class HashEntry {
	Hashable element;
	boolean isActive;
	public HashEntry(Hashable e){this(e, true);
	}
	public HashEntry(Hashable e, boolean i) {
	this.element = e;
	this.isActive = i;
	}
	}
	public class QuadraticProbingHashTable {
	public QuadraticProbingHashable()
	public QuadraticProbingHashable(int size)
	public void makeEmpty( )

	public Hashable find(Hashable x)
	public void insert(Hashable x)
	public void remove(Hashable x)

	public static int hash(String key, int tableSize)
	private static final int DEFAULT_TABLE_SIZE = 11;

	protected HashEntry [ ] array; private int currentSize;
	private void allocateArray(int arraySize )
	private boolean isActive( int currentPos )
	private int findPos( Hashable x )
	private void rehash( )// 需要扩大 hash 表大小的时候，再哈希
	private static int nextPrime( int n )
	private static boolean isPrime( int n )
	}

# 双散列哈希 (Double Hashing)

If hash1(k)= d and the bucket is already occupied then we will counting hash2(k) = c, examine successive buckets d+c, d+2c, d+3c……，in the array

如果 k 的第一哈希值为 d，而这个对应的格子已经被占用则我们继续计算 k 的第二哈希值，然后检查 d+c…

第一个散列函数发生冲突，那么使用第二个散列函数来放置，如果再次冲突则进行相应探测。

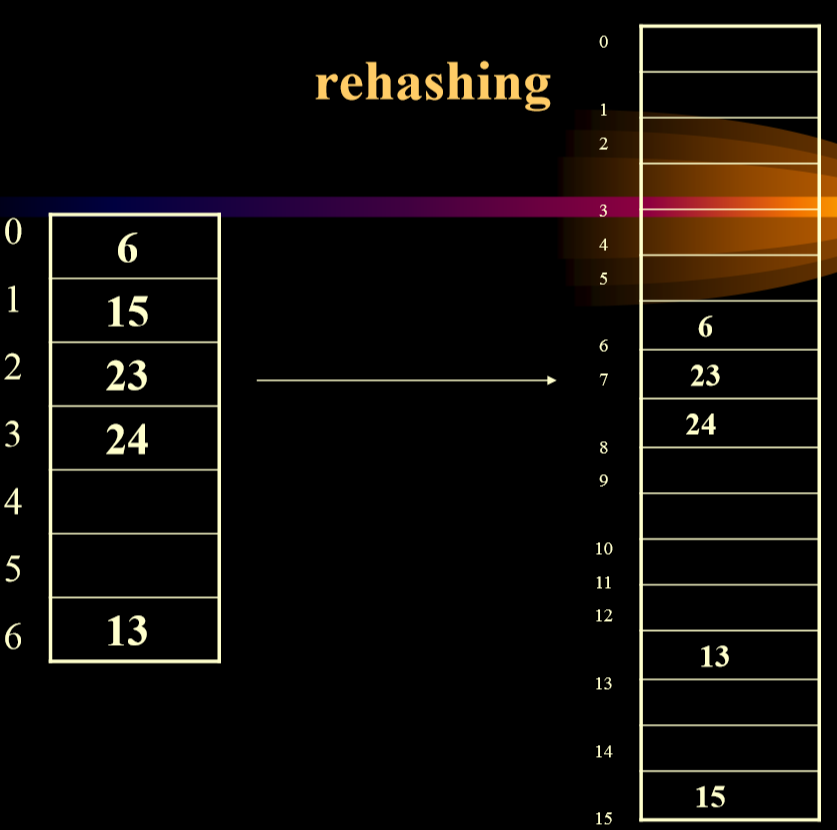
再散列 (进行扩容)

尽量保证表项数 > 表的 70%，也就是意味着如果不满足，就需要进行再散列。

# 再散列的实现

	private void rehash(){
	HashEntry [] oldArray = array ;
	allocateArray(nextPrime(2*oldArray.length));
	currentSize = 0;
	for( int i = 0;i < oldArray.length;i++ )
	if(oldArray[i] != null && oldArray[i].isActive)
	insert(oldArray[i].Element);
	}

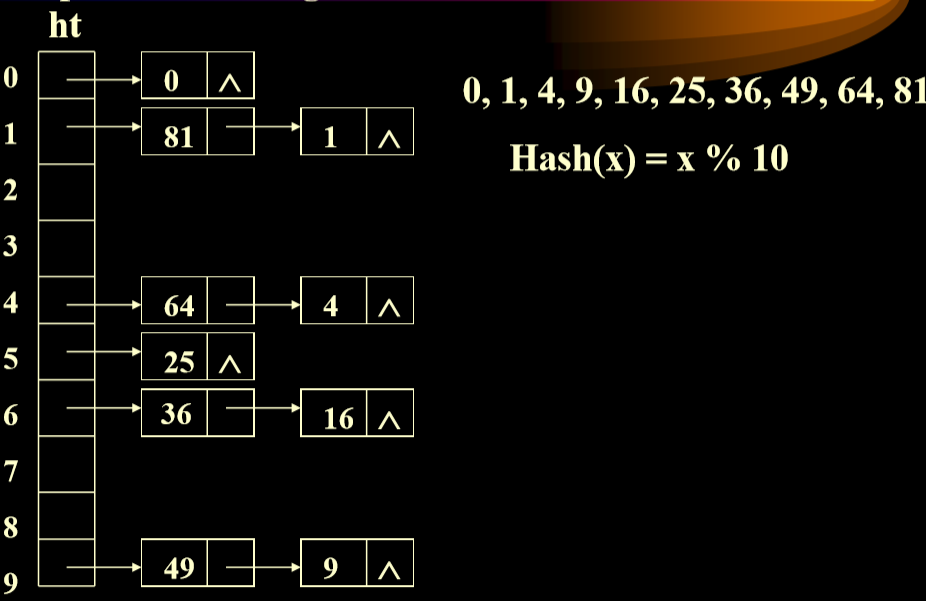
# 分离链接法 (Separate Chaining)

使用每个位置对应线性表解决这个问题，避免了出现向下进行顺延的情况。

# 代码实现

	public class SeparateChainingHashTable {
	public SeparateChainingHashTable( )
	public SeparateChainingHashTable( int size )
	public void insert( Hashable x )
	public void remove( Hashable x )
	public Hashable find( Hashable x )
	public void makeEmpty( )
	public static int hash( String key, int tableSize )

	private static final int DEFAULT_TABLE_SIZE = 101;
	private LinkedList [] theLists;
	private static int nextPrime( int n )
	private static boolean isPrime( int n )
	}

	public interface Hashable{
	int hash( int tableSize );
	}
	public class Employee implements Hashable {
	public int hash( int tableSize ) {
	return SeparateChainingHashTable.hash( name, tableSize );
	}
	public boolean equals( object rhs ) {
	return name.equals( ( Employee) rhs ).name );
	}

	private String name;
	private double salary;
	private int seniority;
	}

	public SeparateChainingHashTable() {
	this( DEFAULT_TABLE_SIZE );
	}
	public SeparateChainingHashTable(int size) {
	theLists = new LinkedList[ nextPrime( size ) ];
	for( int i = 0; i < theLists.length; i++ ) theLists[ i ] = new LinkedList( );
	}
	public void makeEmpty( ) {
	for( int i = 0; i < theLists.length; i++ )
	theLists[ i ].makeEmpty( );
	}
	public void remove( Hashable x ){
	theLists[ x.hash( theLists.length ) ].remove( x );
	}
	public Hashable find( Hashable x ) {
	return ( Hashable ) theLists[ x.hash( theLists.length ) ]. Find( x ). Retrieve( );
	}
	public void insert( Hashable x ) {
	LinkedList whichList = theLists[ x.hash( theLists.length ) ];
	LinkedListItr itr = whichList.find( x );
	if( itr.isPastEnd( ) )
	whichList.insert( x, whichList.zeroth( ) );
	}

数据结构