# 树
- 概念:选择填空
- 完全二叉树的表示法、物理层表示法、链接表示法、游标表示法、静态数组表示法
- 遍历肯定要考:先序中序后序
- 广义表一般不考
- 字符串只有考的很简单的时候才会考,考的概率不大
- 双亲表示法在并查集里会用、会考
- 左子女右兄弟
- 遍历
- 二叉树
- 森林
- 线索化树常考
- 霍夫曼树、霍夫曼编码(偶尔会考,像并查集、散列表
# 数据结构的分类

- 线性的
- 非线性的
# 树的基本定义

- 定义: A tree T is a collection of nodes (element). 树 T 是结点的集合
- The collection can be empty; otherwise, a tree consists of a distinguished node r, called the root, and zero or more nonempty(sub)trees T1, T2, ……, Tk(这个集合可能为空,否则这个树是由一个特殊的根节点和 0 个或多个子树组成)
递归的方式定义 ——
树保证了最坏情形下的时间界,其大部分操作的运行时间平均为 O (log N)。
这种数据结构叫作二叉查找树,是两种库集合类 TreeSet 和 TreeMap 实现的基础。
# 与树有关的概念
# 度
Degree of an elements (node) 节点的度数:有多少个子节点
Degree of a tree 树的度:树里面结点的最大的度数

# 叶
Leaf 叶节点:树里面度数为 0 的节点。
# 分支
Branch 分支节点:树里面度数不为 0 的节点。
# 层
root 的层次为 0 或 1
节点的层次等于其父结点的层次 + 1
# 深度
从根到 Ni 的唯一的路径的长
# 高度
Ni 到一片树叶的最长路径的长
一棵树的高度取决于它根的高度
高度和深度是一样的,最大的层次

# 树的实现
由链表或数组实现
# 二叉树
# 定义
- 二叉树的定义:A binary tree t is a finite (possibly empty) collection of elements.(二叉树 t 是一个有限的节点的集合)
- 二叉树的特点:
- 每个结点最多有两棵子树,即二叉树不存在度大于 2 的结点。
- 二叉树的子树有左右之分,其子树的次序不能颠倒。
每个节点都不能有多于两个的儿子。
Class BinaryNode{ | |
Object element; | |
BinaryNode left; | |
BinaryNode right; | |
} |


# 二叉树的性质 (考前重点)

n 个结点的二叉树之间有 n-1 条边。
第 i 层的节点数最多是 2i 个

高度为 h (从 0 开始计) 的二叉树中结点最少 h+1 个,最多 2h+1-1

如果一颗二叉树有 n0 个树叶,并且结点度数为 2 的节点有 n2 个,则 n0=n2+1 个
n = B + 1
结点数是 1*(一个子节点) + 2 *(两个子节点) + 根节点

有 n 个结点的二叉树的高度最大为 n-1,最小为 log2 (n+1)(向上取整)-1
# 满二叉树

树中每个分支结点(非叶结点)都有两棵非空子树【定义略有不同】
# 完全二叉树

定义:Suppose we number the elements in a full binary tree of height h using the number 1 through 2h+1 (假设我们为一个高度为 h 的满二叉树进行使用 1 - 2h+1 的数字进行编码)
We began at level 0 and go down to level h.Within levels the elements are numbered left to right. (我们从 0 层到 h 层,从上到下,从左到右进行编码)
完全二叉树和满二叉树是不同的,完全二叉树的最后一层可以不全满,但是必须从左开始顺序无空缺。


完全二叉树的性质
# 数组实现
- 其标记为其在数组中的下标,使用数组来存储。
- 常规二叉树的数组表示的位置上一定有空的。
- 很稀疏的二叉树会导致数组存储二叉树有大量的内存空间被浪费掉。

# 链表实现

Linked representation (also called L-R linked storage) 也被称为 L-R 链表存储。
# cursor

# 二叉树的实现





template<class T> void BinaryTree<T>::MakeTree(const T& data, BinaryTree<T>& leftch,BinaryTree<T>& rightch){ | |
root=new BinaryNode<T>(data, leftch.root, rightch.root); | |
leftch.root = rightch.root=0; | |
} | |
template<class T> void BinaryTree<T>::BreakTree(T& data, BinaryTree<T>& leftch,BinaryTree<T>& rightch) | |
{ | |
if(!root) throw BadInput();//tree empty | |
data=root.element; | |
leftch.root=root.Left; rightch.root=root.Right; | |
delete root; | |
root=0; | |
} |
#include<iostream.h> | |
#include <binary.h> | |
int count=0; | |
BinaryTree<int>a,x,y,z; | |
template<class T> | |
void ct(BinaryTreeNode<T>*t){count++;} | |
void main(void) { | |
a.MakeTree(1,0,0); | |
z.MakeTree(2,0,0); | |
x.MakeTree(3,a,z); | |
y.MakeTree(4,x,0); | |
y.PreOrder(ct); | |
cout<<count<<endl; | |
} |
# 二叉树的遍历(递归和迭代访问)
- 以下算法中的二叉树是通过链表实现的。
- Each element is visited exactly once
- V----- 表示访问一个结点 vertice
- L----- 表示访问 V 的左子树 left tree
- R----- 表示访问 V 的右子树 right tree
- 所有的遍历顺序:VLR\LVR、LRV、VRL、RVL、RLV
- 常用的遍历顺序
- 先序遍历:VLR
- 中序遍历:LVR
- 后序遍历:LRV
- 广度优先遍历:先处理树根节点,然后处理靠近的第一层的节点

前序遍历、中序遍历和后序遍历都可用递归 / 非递归实现
前序遍历
![image-20221030181902464]()
中序遍历
![image-20221030182553336]()
![image-20221030182825664]()
后序遍历
![image-20221030182605342]()
后序遍历的非递归法

层序遍历

把子树放到队列里,然后访问子树的下一个节点,弹出子树。
# 创建二叉树


# 利用前序和中序构造一棵二叉树
返回 void

返回 BinaryNode<Type>


# 已知中序与后序,能否唯一构造一颗二叉树?

# 已知先序与后序呢?
# ADT 和类扩展

# height
高度是 max(左子树,右子树)加上 1

# 树的应用

Binary-Tree Representation of a Tree 树的存储方式:三种
- 广义表表示:a (b (f,g),c,d (h,i,j),e)
- 双亲表示法;记下自己的父结点位置,问题是:找子节点需要遍历一遍。
- 左子女 — 右兄弟表示法
# 左子女 - 右兄弟(树变成二叉树)
// 左子女 —— 右兄弟表示法 | |
class TreeNode: | |
T data; | |
TreeNode *firstchild, *nextsibling; | |
class Tree: | |
TreeNode * root, *current; | |
// 在树中创建一个新的节点 | |
template <class T> void Tree <T>::Insertchild(T value) { | |
TreeNode<T>*newnode = new TreeNode<T>(value); | |
if(current->firstchild == NULL) | |
current->firstchild = newnode; | |
else { | |
TreeNode<T>*p = current->firstchild; | |
while ( p->nextsibling!=NULL) | |
p = p->nextsibling; | |
p->nextsibling = newnode; | |
} | |
} |
# 森林变成二叉树



# 树的遍历(深度优先、广度优先)


# 森林的遍历


先转化成二叉树,遍历

广度优先遍历(层次遍历)按照原来的 forest 进行遍历
# string


# 字符串的类说明


# 部分成员函数的实现
子字符串


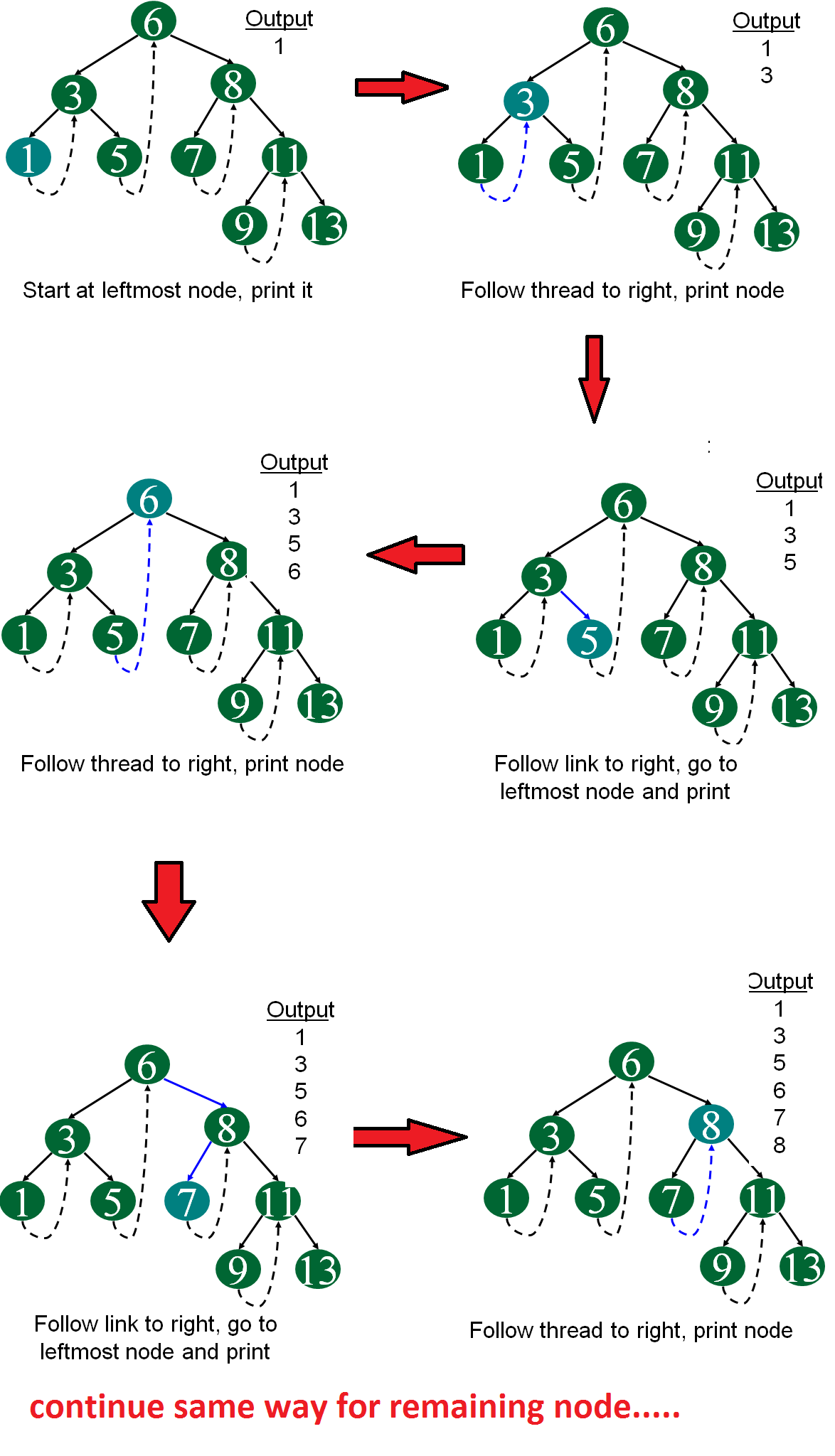
# Thread Binary Tree 线索二叉树
参考链接:https://www.geeksforgeeks.org/threaded-binary-tree/

- 目的:让二叉树遍历的速度更快
- 特点:在树的节点中加入一个指针 (比如指向下一个节点)
- n 个结点的二叉树有 2n 个链域,其中真正有用的是 n–1 个,其它 n+1 个都是空域 (null)。为了充分利用结点中的空域,使得对某些运算更快,如前驱或后继等运算。


定义:在二叉树的结点上加上线索的二叉树称为线索二叉树,对二叉树以某种遍历方式(如先序、中序、后序或层次等)进行遍历,使其变为线索二叉树的过程称为对二叉树进行线索化。
# 存储

注意 0 和 1 所表示的意思
# 类实现


# 按中序遍历中序线索树


// 使用是 current 来记录下来当前节点 | |
template<class Type> ThreadNode<Type>* ThreadInorderIterator<Type>::First() { | |
while (current->leftThread==0){ | |
current = current->leftchild; | |
} | |
return current;// 找中序遍历的第一个节点 | |
} | |
template<class Type> ThreadNode<Type>* ThreadInorderIterator<Type>::Next() { | |
ThreadNode<Type>*p = current->rightchild;// 可能是右子树的根节点,也可能是右链 | |
if(current->rightThread==0) | |
while(p->leftThread==0){ | |
// 如果有右子树就要搜索到最左下部分 | |
p=p->leftchlid; | |
} | |
current=p; | |
} | |
template<class Type> void ThreadInorderIterator<Type>:: Inorder() { | |
ThreadNode<Type> *p; | |
for ( p=Frist(); p!=NULL; p=Next()) | |
cout<< p->data << endl; | |
} |
# 构造中序线索树

pre 指针,构建前驱、后继指针

# 构建代码
Void Inthread(threadNode<T> * T) { | |
stack <threadNode <T>*> s(10) | |
ThreadNode <T> *p = T ; | |
ThreadNode <T> *pre = NULL; | |
for (;;) { | |
// 查找到最左下部分的 | |
while (p!=NULL) { | |
s.push(p); | |
p = p ->leftchild; | |
} | |
// 开始弹出栈 | |
if (!s.IsEmpty()){ | |
p = s.pop; | |
if (pre != NULL) { | |
// 添加的代码,在这时候处理 pre | |
if (pre ->rightchild == NULL){ | |
pre ->rightchild = p; | |
pre ->rightthread = 1; | |
} | |
// 处理 p | |
if( p -> leftchild == NULL) { | |
p -> leftchild = pre; | |
p ->leftthread = 1; | |
}// 添加的代码 | |
} | |
pre = p ; | |
p = p -> rightchild ; | |
} | |
else return; | |
}//for | |
}// 建议把 pre 和 p 存储成全局变量 |


这里可以和之前的中序遍历相比较,可以看出,就是多处理了 pre 的内容
# 增长树与霍夫曼树 Huffman Tree


外通路长度
内通路长度
结点的带权路径长度

11 + 8 + 6 + 9 = 34
6 + 12 +33 +2 = 53
4 + 22 + 6 + 8 = 40
# 霍夫曼算法

外接点权值相等,考虑内节点的权值
# 霍夫曼编码


哈夫曼树的参考资料 https://zhuanlan.zhihu.com/p/154356949
对应的霍夫曼树
1)将看成是有 n 棵树的森林,每一棵树都只有一个根节点
2)在这个森林中选择权值最小的两棵树进行合并,得到一颗新的树,这两颗树作为新树的左右子树,新树的根节点权重为左右子树的根节点权重之和。
3)将之前的根节点权重最小的两棵树从森林删除,并把步骤 2 产生的新树加入森林
4)重复步骤 2 和步骤 3,直到森林只有一棵树为止。

# 广义表
一般不考
# 查找树 ADT—— 二叉查找树
- 值不重复
- 若它的左子树不为空,则左子树上所有结点的值都小于根结点的值。
- 若它的右子树不为空,则右子树上所有结点的值都大于根结点的值。
- 它的左右子树也分别是二叉搜索树。
删除有三种情况

java.lang.Comparable :在类定义的时候,可以实现好的接口,里面有 compareTo 这个方法需要实现。
# 带索引的二叉搜索树 Indexed Binary Tree
# 力扣题
# 94 二叉树的中序遍历
# 递归实现
#include <stdio.h> | |
#include <iostream> | |
#include <vector> | |
using namespace std; | |
struct TreeNode { | |
int val; | |
TreeNode *left; | |
TreeNode *right; | |
TreeNode() : val(0), left(nullptr), right(nullptr) {} | |
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} | |
TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} | |
}; | |
class Solution { | |
public: | |
vector<int> inorderTraversal(TreeNode* root) { | |
if(root == nullptr) return vector<int>(); | |
vector<int> left = inorderTraversal(root->left); | |
left.push_back(root->val); | |
vector<int> right = inorderTraversal(root->right); | |
left.insert(left.end(), right.begin(), right.end()); | |
return left; | |
} | |
}; |
An Arrow operator in C/C++ allows to access elements in Structures and Unions. It is used with a pointer variable pointing to a structure or union. The arrow operator is formed by using a minus sign, followed by the greater than symbol as shown below.
Syntax:
(pointer_name)->(variable_name)
Operation: The -> operator in C or C++ gives the value held by variable_name to structure or union variable pointer_name.
Difference between Dot(.) and Arrow(->) operator:
. 和 -> 的区别
- The Dot(.) operator is used to normally access members of a structure or union.
- The Arrow(->) operator exists to access the members of the structure or the unions using pointers.
# 迭代实现【有点问题】
class Solution { | |
public: | |
vector<int> inorderTraversal(TreeNode* root) { | |
vector<int> ans; | |
stack<TreeNode*> stk; | |
for( ; ; ){ | |
while(root != nullptr){ | |
stk.push(root); | |
root = root -> left; | |
} | |
if(!stk.empty()){ | |
root = stk.top(); | |
stk.pop(); | |
ans.push_back(root->val); | |
root = root -> right; | |
}else{ | |
return ans; | |
} | |
} | |
} | |
}; |
stack 的 pop 没有返回值
需要先 top 在 pop
# Morris 遍历算法实现
Morris 遍历的详细解释 + 注释版
一些前置知识:
- 前驱节点,如果按照中序遍历访问树,访问的结果为 ABC,则称 A 为 B 的前驱节点,B 为 C 的前驱节点。
- 前驱节点 pre 是 curr 左子树的最右子树(按照中序遍历走一遍就知道了)。
- 由此可知,前驱节点的右子节点一定为空。
主要思想:
树的链接是单向的,从根节点出发,只有通往子节点的单向路程。
中序遍历迭代法的难点就在于,需要先访问当前节点的左子树,才能访问当前节点。
但是只有通往左子树的单向路程,而没有回程路,因此无法进行下去,除非用额外的数据结构记录下回程的路。
在这里可以利用当前节点的前驱节点,建立回程的路,也不需要消耗额外的空间。
根据前置知识的分析,当前节点的前驱节点的右子节点是为空的,因此可以用其保存回程的路。
但是要注意,这是建立在破坏了树的结构的基础上的,因此我们最后还有一步 “消除链接”’的步骤,将树的结构还原。
重点过程: 当遍历到当前节点 curr 时,使用 cuur 的前驱节点 pre
- 标记当前节点是否访问过
- 记录回溯到 curr 的路径(访问完 pre 以后,就应该访问 curr 了)
以下为我们访问 curr 节点需要做的事儿:
- 访问 curr 的节点时候,先找其前驱节点 pre
- 找到前驱节点 pre 以后,我们根据其右指针的值,来判断 curr 的访问状态:
- pre 的右子节点为空,说明 curr 第一次访问,其左子树还没有访问,此时我们应该将其指向 curr,并访问 curr 的左子树
- pre 的右子节点指向 curr,那么说明这是第二次访问 curr 了,也就是说其左子树已经访问完了,此时将 curr.val 加入结果集中
更加细节的逻辑请参考代码:
public List<Integer> Morris(TreeNode root) { | |
List<Integer> ans=new LinkedList<>(); | |
while(root!=null){ | |
// 没有左子树,直接访问该节点,再访问右子树 | |
if(root.left==null){ | |
ans.add(root.val); | |
root=root.right; | |
}else{ | |
// 有左子树,找前驱节点,判断是第一次访问还是第二次访问 | |
TreeNode pre=root.left; | |
while(pre.right!=null&&pre.right!=root) | |
pre=pre.right; | |
// 是第一次访问,访问左子树 | |
if(pre.right==null){ | |
pre.right=root; | |
root=root.left; | |
} | |
// 第二次访问了,那么应当消除链接 | |
// 该节点访问完了,接下来应该访问其右子树 | |
else{ | |
pre.right=null; | |
ans.add(root.val); | |
root=root.right; | |
} | |
} | |
} | |
return ans; | |
} |
# 144 二叉树的前序遍历
递归方法
// 树的定义同前 | |
class Solution { | |
public: | |
vector<int> preorderTraversal(TreeNode* root) { | |
if(root == nullptr) return vector<int>(); | |
vector<int> left = preorderTraversal(root->left); | |
left.insert(left.begin() , root->val); | |
vector<int> right = preorderTraversal(root->right); | |
left.insert(left.end(), right.begin(), right.end()); | |
return left; | |
} | |
}; |
迭代方法
class Solution { | |
public: | |
vector<int> preorderTraversal(TreeNode* root) { | |
vector<int> res; | |
if (root == nullptr) { | |
return res; | |
} | |
stack<TreeNode*> stk; | |
TreeNode* node = root; | |
while (!stk.empty() || node != nullptr) { | |
while (node != nullptr) { | |
res.emplace_back(node->val); | |
stk.emplace(node); | |
node = node->left; | |
} | |
node = stk.top(); | |
stk.pop(); | |
node = node->right; | |
} | |
return res; | |
} | |
}; |
emplace_back () 和 push_back () 的区别,就在于底层实现的机制不同。push_back () 向容器尾部添加元素时,首先会创建这个元素,然后再将这个元素拷贝或者移动到容器中(如果是拷贝的话,事后会自行销毁先前创建的这个元素);而 emplace_back () 在实现时,则是直接在容器尾部创建这个元素,省去了拷贝或移动元素的过程。
# 145 二叉树的后序遍历
递归
class Solution { | |
public: | |
vector<int> postorderTraversal(TreeNode* root) { | |
if(root == nullptr) return vector<int>(); | |
vector<int> left = postorderTraversal(root -> left); | |
vector<int> right = postorderTraversal(root -> right); | |
left.insert(left.end(), right.begin(), right.end()); | |
left.push_back(root -> val); | |
return left; | |
} | |
}; |
迭代
class Solution { | |
public: | |
vector<int> postorderTraversal(TreeNode* root) { | |
if(root == nullptr) return vector<int>(); | |
vector<int> ans; | |
stack<TreeNode*> stk; | |
TreeNode* prev = nullptr; | |
while(!stk.empty() || root != nullptr){ | |
while(root != nullptr){ | |
stk.push(root); | |
root = root -> left; | |
} | |
root = stk.top(); | |
stk.pop(); | |
if(root -> right == nullptr || root -> right == prev){ | |
ans.push_back(root -> val); | |
prev = root; | |
root = nullptr; | |
}else{ | |
stk.push(root); | |
root = root -> right; | |
} | |
} | |
return ans; | |
} | |
}; |



